Fused Softmax

In this tutorial, you will write a fused softmax operation that is significantly faster than PyTorch’s native op for a particular class of matrices: those whose rows can fit in the GPU’s SRAM. You will learn about:

• The benefits of kernel fusion for bandwidth-bound operations.

• Reduction operators in Triton.

Motivations

Custom GPU kernels for elementwise additions are educationally valuable but won’t get you very far in practice. Let us consider instead the case of a simple (numerically stabilized) softmax operation:

import torch


# Compute the row-wise softmax of x
@torch.jit.script
def naive_softmax(x):
    # read  MN elements ; write M  elements
    x_max = x.max(dim=1)[0]
    # read 2MN elements ; write MN elements
    z = x - x_max[:, None]
    # read  MN elements ; write MN elements
    numerator = torch.exp(x)
    # read  MN elements ; write M  elements
    denominator = numerator.sum(dim=1)
    # read 2MN elements ; write MN elements
    ret = numerator / denominator[:, None]
    # in total: read 7MN elements ; wrote 3MN + 2M elements
    return ret

When implemented naively in pytorch, computing y = naive_softmax(x) for \(x \in R^{M \times N}\) requires reading \(7MN\) elements from DRAM and writing back \(3MN + 2M\) elements. This is obviously wasteful; we’d prefer to have a custom “fused” kernel that only reads X once and does all the necessary computations on-chip. Doing so would require reading and writing back only \(MN\) bytes, so we could expect a theoretical speed-up of ~5x (i.e., \((10MN + 2M) / 2MN\)). The torch.jit.script flags aims to perform this kind of “kernel fusion” automatically but, as we will see later, it is still far from ideal.

Compute Kernel

Our softmax kernel works as follows: each program loads a row of the input matrix X, normalizes it and writes back the result to the output Y. Note that one important limitation of Triton is that each block must have a power-of-two number of elements, so we need to internally “pad” each row and guard the memory operations properly if we want to handle any possible input shapes:

import triton
import triton.language as tl


@triton.jit
def _softmax(Y, X, stride_xm, stride_ym, M, N, **meta):
    # row index
    m = tl.program_id(0)
    # col indices
    # here BLOCK is the smallest power of two greater than `N`
    n = tl.arange(0, meta['BLOCK'])
    # the memory address of all the elements
    # that we want to load can be computed as follows
    X = X + m * stride_xm + n
    x = tl.load(X, mask=n < N, other=-float('inf'))
    # Substract maximum for numerical stability
    z = x - tl.max(x, axis=0)
    # Note that exponentials in Triton are fast
    # but approximate (i.e., think __expf in CUDA)
    num = tl.exp(z)
    denom = tl.sum(num, axis=0)
    y = num / denom
    # Write back to Y
    Y = Y + m * stride_ym + n
    tl.store(Y, y, mask=n < N)

We can create a helper function that enqueues the kernel and its (meta-)arguments for any given input tensor.

def next_power_of_2(n):
    n -= 1
    n |= n >> 1
    n |= n >> 2
    n |= n >> 4
    n |= n >> 8
    n |= n >> 16
    n += 1
    return n


def softmax(x):
    M, N = x.shape
    # The block size is the smallest power of two greater than the number of columns in `x`
    BLOCK = next_power_of_2(N)
    # Another trick we can use is to ask the compiler to use more threads per row by
    # increasing the number of warps (`num_warps`) over which each row is distributed.
    # You will see in the next tutorial how to auto-tune this value in a more natural
    # way so you don't have to come up with manual heuristics yourself.
    num_warps = 4
    if BLOCK >= 2048: num_warps = 8
    if BLOCK >= 4096: num_warps = 16
    # Allocate output
    y = torch.empty_like(x)
    # Enqueue kernel. The launch grid is simple: we have one kernel instance per row of the input matrix
    _softmax[(M, )](y, x, x.stride(0), y.stride(0), M, N, num_warps=num_warps, BLOCK=BLOCK)
    return y

Unit Test

We make sure that we test our kernel on a matrix with an irregular number of rows and columns. This will allow us to verify that our padding mechanism works.

torch.manual_seed(0)
x = torch.randn(1823, 781, device='cuda')
y_tri = softmax(x)
y_ref = torch.softmax(x, axis=1)
print(torch.allclose(y_tri, y_ref))

Out:

True

As expected, the results are identical.

Benchmark

Here we will benchmark our operation as a function of the number of columns in the input matrix – assuming 4096 rows. We will then compare its performance against (1) torch.softmax and (2) the naive_softmax defined above.

@triton.testing.perf_report(
    triton.testing.Benchmark(
        x_names=['N'],  # argument names to use as an x-axis for the plot
        x_vals=[128 * i for i in range(2, 100)],  # different possible values for `x_name`
        line_arg='provider',  # argument name whose value corresponds to a different line in the plot
        line_vals=['triton', 'torch-native', 'torch-jit'],  # possible values for `line_arg``
        line_names=["Triton", "Torch (native)", "Torch (jit)"],  # label name for the lines
        styles=[('blue', '-'), ('green', '-'), ('green', '--')],  # line styles
        ylabel="GB/s",  # label name for the y-axis
        plot_name="softmax-performance",  # name for the plot. Used also as a file name for saving the plot.
        args={'M': 4096}  # values for function arguments not in `x_names` and `y_name`
    )
)
def benchmark(M, N, provider):
    x = torch.randn(M, N, device='cuda', dtype=torch.float32)
    if provider == 'torch-native':
        ms, min_ms, max_ms = triton.testing.do_bench(lambda: torch.softmax(x, axis=-1))
    if provider == 'triton':
        ms, min_ms, max_ms = triton.testing.do_bench(lambda: softmax(x))
    if provider == 'torch-jit':
        ms, min_ms, max_ms = triton.testing.do_bench(lambda: naive_softmax(x))
    gbps = lambda ms: 2 * x.nelement() * x.element_size() * 1e-9 / (ms * 1e-3)
    return gbps(ms), gbps(max_ms), gbps(min_ms)


benchmark.run(show_plots=True, print_data=True)

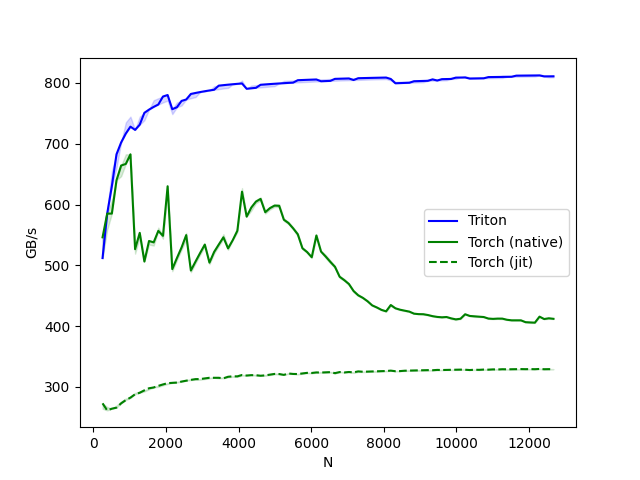
Out:

softmax-performance:
          N      Triton  Torch (native)  Torch (jit)
0     256.0  512.000001      546.133347   273.066674
1     384.0  585.142862      585.142862   261.446801
2     512.0  630.153853      585.142849   264.258068
3     640.0  682.666684      640.000002   265.974036
4     768.0  702.171410      664.216187   273.066663
..      ...         ...             ...          ...
93  12160.0  812.359066      405.755985   329.204728
94  12288.0  812.429770      415.661740   329.602681
95  12416.0  810.840807      411.722274   329.173158
96  12544.0  810.925276      412.971190   329.292871
97  12672.0  811.007961      412.097543   329.142870

[98 rows x 4 columns]

In the above plot, we can see that:

• Triton is 2-3x faster than the Torch JIT.

• Triton is even faster than torch.softmax. My guess from looking at the source-code of the PyTorch kernel is that PyTorch only partially fuses the computation of the softmax. This means that – when temporary data is too large to fit entirely in the GPU’s cache – it transfers almost twice the amount of memory necessary. Note that our Triton kernel is not only faster than PyTorch’s CUDA kernel, it is also easier to read, understand and maintain.